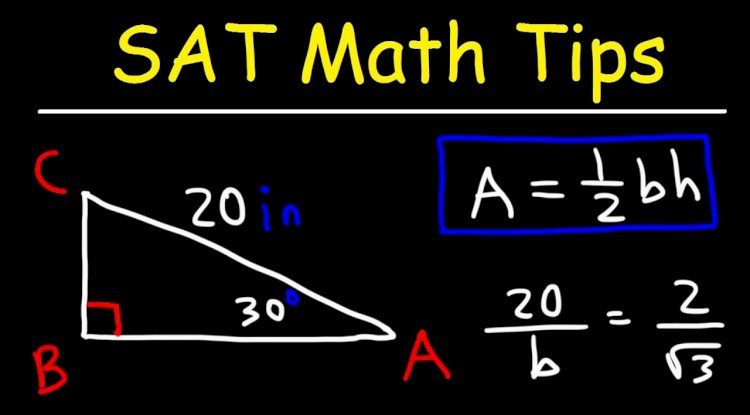
SAT Math: Formül Listesi
Digital SAT Math için tek sayfalık formül özeti: cebir kuralları, doğrusal–kuadratik–üstel fonksiyonlar, yüzde–oran, istatistik, olasılık, geometri ve trigonometri. Zaman yönetimi ve birim–işaret kontrol ipuçlarıyla.
Notasyon & Hızlı İpuçları
-
Birim–İşaret–Aralık (BİA): Son adımda daima birim, işaret (+/−) ve istenen aralığı kontrol et.
-
Doğrulama: Şıkları yerine koyma / sınır denemesi / oran–ölçek ile hızlı ele.
-
Dönüşümler: (y=a,f(b(x-h))+k) → dikey ölçek a, yatay ölçek 1/b, sağa–sola h, yukarı–aşağı k.
1) Cebir – Sayılar & Üslü–Köklü–Log
Temel Özellikler
-
Dağılma: (a(b+c)=ab+ac)
-
Ortak çarpan: (ab+ac=a(b+c))
-
Mutlak değer: (|x|=\begin{cases}x&x\ge 0\-x&x<0\end{cases})
Üs Kuralları
-
(a^m\cdot a^n=a^{m+n}) · ( \dfrac{a^m}{a^n}=a^{m-n}) · ((a^m)^n=a^{mn})
-
(a^{-n}=\dfrac{1}{a^n}) · (a^{1/n}=\sqrt[n]{a})
Köklü Dönüşümler
-
(\sqrt{ab}=\sqrt a,\sqrt b) (a,b≥0) · (\sqrt{\dfrac{a}{b}}=\dfrac{\sqrt a}{\sqrt b})
Logaritmalar (gerekli kadar)
-
(\log_b(xy)=\log_b x+\log_b y) · (\log_b!\left(\dfrac{x}{y}\right)=\log_b x-\log_b y)
-
(\log_b(x^k)=k\log_b x) · Taban değişimi: (\displaystyle \log_b a=\frac{\log a}{\log b})
2) Doğrular & Doğrusal Modeller
Eğim–Kesişim
-
(y=mx+n) (eğim (m), (y)-kesişim (n))
-
Eğim iki noktadan: (m=\dfrac{y_2-y_1}{x_2-x_1})
Noktadan Geçen Doğru
-
(y-y_1=m(x-x_1))
Paralel/ Diken
-
Paralel doğrular: eğimler eşit.
-
Dik doğrular: (m_1\cdot m_2=-1).
Orantı / Doğrusal Orantı
-
(y=kx) → orantı sabiti (k).
3) Kuadratikler (Quadratics)
Formlar
-
Standart: (y=ax^2+bx+c)
-
Tepe (vertex): (y=a(x-h)^2+k), tepe ( (h,k))
-
Çarpanlarına ayrılmış: (y=a(x-r_1)(x-r_2)) (kökler (r_1,r_2))
Formüller
-
Kökler: (\displaystyle x=\frac{-b\pm\sqrt{b^2-4ac}}{2a})
-
Ayrımcı (discriminant): (\Delta=b^2-4ac)
-
Tepe noktası: (h=-\dfrac{b}{2a}), (k=f(h))
-
Köklerin toplamı/çarpımı: (r_1+r_2=-\dfrac{b}{a}), (r_1r_2=\dfrac{c}{a})
4) Fonksiyonlar – Dönüşüm, Bileşim, Ters
-
Dönüşüm genel kuralı: (y=a,f(b(x-h))+k)
-
Genlik/dikey ölçek (a); yatay ölçek (1/b); sağa–sola (h); yukarı–aşağı (k).
-
-
Bileşim: ((f\circ g)(x)=f(g(x)))
-
Ters (uygunsa): (f^{-1}(y)=x) için (f(f^{-1}(x))=x) (tek değerli ve birebir bölgelerde)
5) Üstel & Büyüme–Azalma
-
Genel: (y=A\cdot b^{x}) (b>1 büyüme, 0<b<1 azalma)
-
Sabit yüzde değişim: ( \text{Yeni}=\text{Eski}\cdot(1\pm r) )
-
Yarım ömür: (y=A\cdot\left(\tfrac12\right)^{t/T_{1/2}})
6) Diziler (Sequences)
-
Aritmetik dizi:
-
Genel terim: (a_n=a_1+(n-1)d)
-
İlk n toplam: (S_n=\dfrac{n}{2}(a_1+a_n)=\dfrac{n}{2}\big(2a_1+(n-1)d\big))
-
-
Geometrik dizi:
-
Genel terim: (a_n=a_1\cdot r^{,n-1})
-
İlk n toplam (r≠1): (S_n=a_1\cdot\dfrac{1-r^{,n}}{1-r})
-
7) Oran–Yüzde–Orantı & Orta Değerler
-
Yüzde Değişim: (\dfrac{\text{Yeni}-\text{Eski}}{\text{Eski}}\times 100%)
-
Ağırlıklı ortalama: (\displaystyle \bar x=\dfrac{\sum w_i x_i}{\sum w_i})
-
Hız–Mesafe–Zaman: (D=RT) (Average speed (=) toplam mesafe / toplam süre)
-
Karışım/Orantı: (\dfrac{a}{b}=\dfrac{c}{d}\Rightarrow ad=bc)
8) İstatistik & Veri Analizi
-
Ortalamalar:
-
Aritmetik ortalama: (\bar x=\dfrac{\sum x_i}{n})
-
Medyan: sıralı verinin ortası; mod: en sık değer
-
-
Yayılım:
-
Aralık = max−min
-
IQR = Q3 − Q1
-
Standart sapma (yorum): dağılım genişledikçe artar.
-
-
Doğrusal Regresyon: ( \hat y=a+bx )
-
(b) (eğim) = x bir arttığında y’nin beklenen değişimi
-
Korelasyon (r): işaret yönü, |r| büyüklük (neden–sonuç değildir).
-
-
Olasılık Temel:
-
(P(A^c)=1-P(A))
-
(P(A\cup B)=P(A)+P(B)-P(A\cap B))
-
Koşullu: (P(A\mid B)=\dfrac{P(A\cap B)}{P(B)})
-
9) Geometri – Düzlem
Açı ve Paralel Doğrular
-
İç–ters, iç–aynı yanda, yöndeş açılar; paralel doğrularda açı ilişkileri.
Üçgen Temelleri
-
İç açılar toplamı (180^\circ)
-
Benzerlik: karşılık gelen kenarlar orantılı, açılar eş
-
Alan: (A=\tfrac12 bh)
Özel Dik Üçgenler
-
Pisagor: (a^2+b^2=c^2)
-
45–45–90: kenar (s) → hipotenüs (s\sqrt2)
-
30–60–90: kısa (s) → hipotenüs (2s), uzun (s\sqrt3)
Dörtgenler
-
Paralelkenar: (A=bh)
-
Dikdörtgen: (A=lw), çevre (2(l+w))
-
Yamuk: (A=\dfrac{(b_1+b_2)}{2},h)
-
Çokgen iç açılar toplamı: ((n-2)\cdot 180^\circ)
Daire
-
Çevre: (C=2\pi r) · Alan: (A=\pi r^2)
-
Yay uzunluğu: (s=r\theta) (radyan), (s=\dfrac{\theta^\circ}{360^\circ}\cdot 2\pi r)
-
Sektör alanı: (A_{\text{sekt}}=\tfrac12 r^2\theta) (radyan), (=\dfrac{\theta^\circ}{360^\circ}\cdot \pi r^2)
10) Geometri – Analitik (Koordinat)
-
Uzaklık: (d=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2})
-
Orta nokta: (\Big(\dfrac{x_1+x_2}{2},,\dfrac{y_1+y_2}{2}\Big))
-
Çember denklemi: ((x-h)^2+(y-k)^2=r^2)
11) Trigonometri (SAT düzeyi)
-
SOH–CAH–TOA:
-
(\sin \theta=\dfrac{\text{karşı}}{\text{hipotenüs}})
-
(\cos \theta=\dfrac{\text{komşu}}{\text{hipotenüs}})
-
(\tan \theta=\dfrac{\text{karşı}}{\text{komşu}})
-
-
Temel özdeşlik: (\sin^2\theta+\cos^2\theta=1)
-
Tamamlayıcı: (\sin(90^\circ-\theta)=\cos\theta)
-
Radyan–derece: ( \pi \text{ rad}=180^\circ ), ( \theta_{\text{rad}}=\theta^\circ\cdot \tfrac{\pi}{180} )
12) Katı Cisimler (hacim – sık sorulanlar)
-
Dik prizma: (V=lwh)
-
Silindir: (V=\pi r^2 h)
-
Koni: (V=\tfrac13 \pi r^2 h)
-
Küre: (V=\tfrac{4}{3}\pi r^3)
13) “Grid-In” (Serbest Cevap) İçin Biçim Kontrolü
-
İstenen biçim (kesir/ondalık), işaret ve aralık şartını son adımda tekrar oku.
-
Yaklaşıklık isteniyorsa, ondalık basamak sınırı veya birim dönüşümüne dikkat.
14) Mini Kontrol Listesi (Sınav Anı)
-
Kökte istenen/koşul kutulu mu?
-
BİA yapıldı mı (Birim–İşaret–Aralık)?
-
90–120 sn’de ilerleme yoksa bayrakla–geç.
-
Şık eleme (en az 2 şık) uygulandı mı?
-
Uzun soruda yöntem seçimi: cebir / grafik / tablo.
Tepkiniz Nedir?